求解如下常微分方程：
$$
\begin{aligned}
\begin{cases}
\frac{du}{dt}=-\frac{u}{t},1\leq t\leq 2, \\
u(1)=1
\end{cases}
\end{aligned}
$$
精确解
将原方程化为$tdu+udt=0$，则有$d(ut)=0$，解得$ut=C$($C$为常数)，代入初始条件得$C=1$，从而该方程的精确解为： $$ \begin{aligned} u=\frac{1}{t},(1\leq t \leq2). \end{aligned} $$
欧拉方法
代入欧拉格式得： $$ \begin{aligned} u_{i+1}=u_{i}+hf(t_i,u_i)=u_i+h(-\frac{u_i}{t_i}) \end{aligned} $$
隐式欧拉方法
由隐式欧拉格式得： $$ \begin{aligned} u_{i+1}=u_{i}+hf(t_{i+1},u_{i+1})=u_i+h(-\frac{u_{i+1}}{t_{i+1}})， \end{aligned} $$ 移项化简可得： $$ \begin{aligned} u_{i+1}=\frac{t_{i+1}u_i}{t_{i+1}+h} \end{aligned} $$
程序
根据上述推导，用python编写程序，代码如下：
# implict euler method
import numpy as np
import matplotlib.pyplot as plt
# the right term of the ODE
def f(t, u):
f = -u/t
return f
# the exact solution of ODE
def fexact(t):
fexact = 1/t
return fexact
N = 100
t_n = 2.0
dt = (t_n - 1.0) / N
t = np.arange(1.0, t_n + dt, dt)
u_euler = np.arange(1.0, t_n + dt, dt)
u = np.arange(1.0, t_n + dt, dt)
u_true = np.arange(1.0, t_n + dt, dt)
i = 0
while i < N:
t[i+1] = t[i] + dt
u_euler[i+1] = u_euler[i] + dt * f(t[i], u_euler[i])
u[i+1] = (u[i] * t[i+1])/(t[i+1] + dt)
u_true[i+1] = fexact(t[i+1])
i = i + 1
err_euler = max(abs(u_euler - u_true))
err_implict_euler = max(abs(u - u_true))
print("The error of euler method: ",err_euler)
print("The error of implict euler method: ",err_implict_euler)
# begin drawing
plt.title('Result')
plt.plot(t, u_euler, color='green', label='euler')
plt.plot(t, u, color='blue', label='implict euler')
plt.plot(t, u_true, color='red', label='exact')
plt.legend() # show the legend
plt.xlabel('t')
plt.ylabel('u')
plt.show()
结果分析
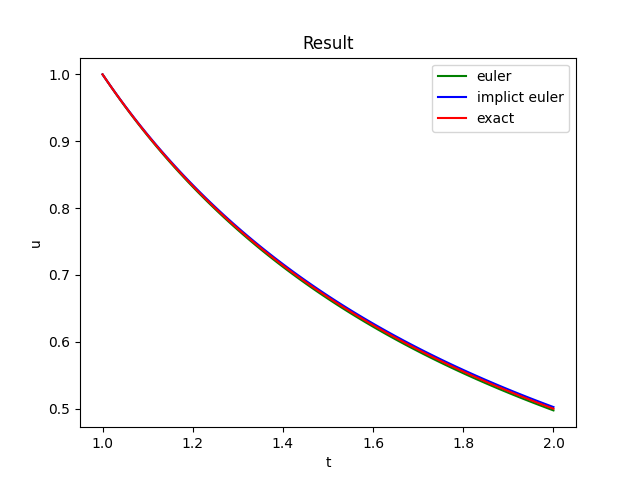
当取$h=0.01$时，此时欧拉方法的误差为0.02631578947368396，隐式欧拉方法的误差为0.023809523809523836，结果如下图所示：
当取不同$h$，得到的误差如下表所示：
| $h$ | 欧拉方法 | 隐式欧拉方法 |
|---|---|---|
| $\frac{1}{2}$ | 0.16666666666666663 | 0.09999999999999998 |
| $\frac{1}{4}$ | 0.0714285714285714 | 0.05555555555555558 |
| $\frac{1}{8}$ | 0.033333333333333215 | 0.02941176470588236 |
| $\frac{1}{16}$ | 0.01612903225806467 | 0.015151515151515138 |
| $\frac{1}{32}$ | 0.00793650793650813 | 0.007692307692307665 |
| $\frac{1}{64}$ | 0.0039370078740155193 | 0.003875968992248069 |