最简显格式
对于如下热传导方程： $$ \begin{cases} \frac{\partial u}{\partial t} =\frac{\partial ^2 u}{\partial t} \quad 0<t<0.03,0<x<1 \\ u(x,0)=\sin(4\pi x) \quad 0 \le x \le 1 \\ u(0,t) = 0 \quad 0 \le t \le 0.03 \\ u(1,t) = 0 \quad 0 \le t \le 0.03 \end{cases} $$
该方程的精确解为$u(t,x)=e^{-(4\pi)^2t}\sin (4 \pi x),0\le t \le 0.03, 0 \le x \le 1.$
首先对时间及空间进行划分，将时间划分为$m-1$份，将空间划分为$n-1$份，则$\tau=\frac{0.03}{m-1},h=\frac{1}{n-1}$。 根据最简显格式可以得到： $$ u_j^{i+1}=\frac{\tau}{h^2}(u_{j+1}^{i}-2u_j^i+u_{j-1}^i)+u_j^{i}, $$ 其中$i=0,1,\cdots,m-1$，$j=0,1,\cdots,n-1$。
编程实现
根据理论推导，用python编写程序如下：
# -*- coding: utf-8 -*-
"""
Created on Sun May 23 11:16:13 2021
@author: XieWenjin
"""
import math
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
t = 0.03 # 时间范围
x = 1.0 # 空间范围
m = input("请输入m：")
m = int(m)
n = input("请输入n：")
n = int(n)
# m = 320 # 时间方向分为320个格子
# n = 64 # 空间方向的格子数
dt = t / (m - 1) # 时间步长
dx = x / (n - 1) # 空间步长
def generate_u(m,n):
u = np.zeros([m,n])
# 边界条件
for j in range(n):
u[0,j] = math.sin(4 * math.pi * j * dx)
for i in range(m):
u[i,0] = 0
u[i,-1] = 0
# 差分法
for i in range(m - 1):
for j in range(1,n - 1):
u[i+1, j] = dt * (u[i, j + 1] + u[i, j - 1] - 2 * u[i, j]) / dx ** 2 + u[i, j]
return u
def drawing(X,Y,Z):
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
plt.show()
def error(u,u_exact):
err = abs(u - u_exact)
return max(map(max, err))
X = np.arange(0, t + dt, dt) # remark:t+dt,not t
Y = np.arange(0, x + dx, dx)
X, Y = np.meshgrid(X, Y)
u_exact = np.exp(- (4*np.pi)**2*X)*np.sin(4*np.pi*Y)
u = generate_u(m,n)
u = np.transpose(u) # 注意这里是转置，而不是np.reshape(u,(n,m))
# print(m,n)
print(error(u,u_exact))
drawing(X,Y,u) # 数值解
# drawing(X,Y,u_exact) # 精确解
# drawing(X,Y,abs(u-u_exact)) # 数值解与精确解之差的绝对值
结果分析
当取$m=320,n=64$时，得到数值解$[u]$如下图所示：
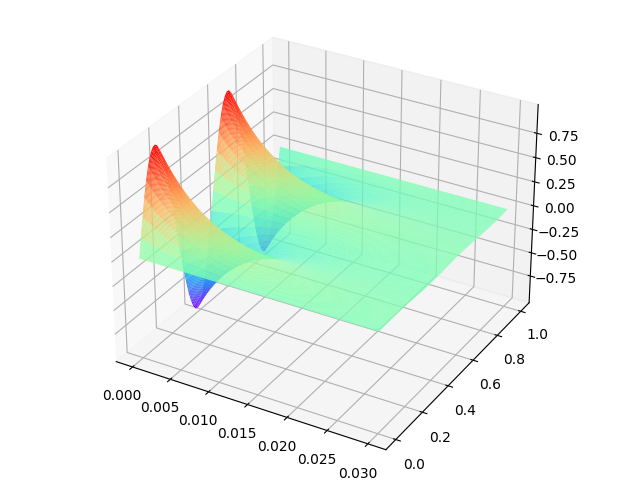
精确解$u$如下图所示：
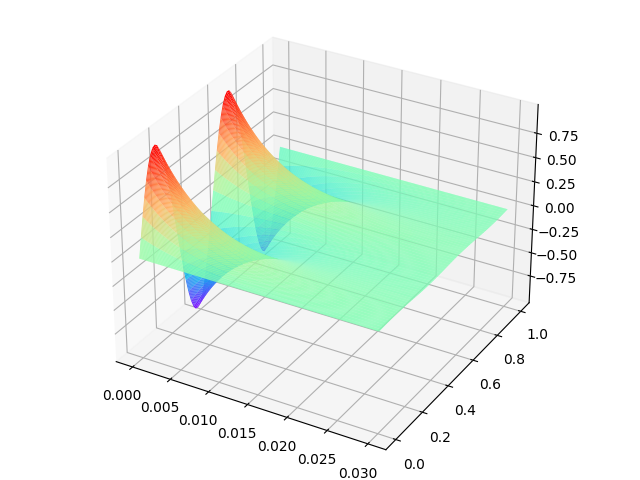
精确解与数值解之差的绝对值$||u-[u]||$如下图所示：
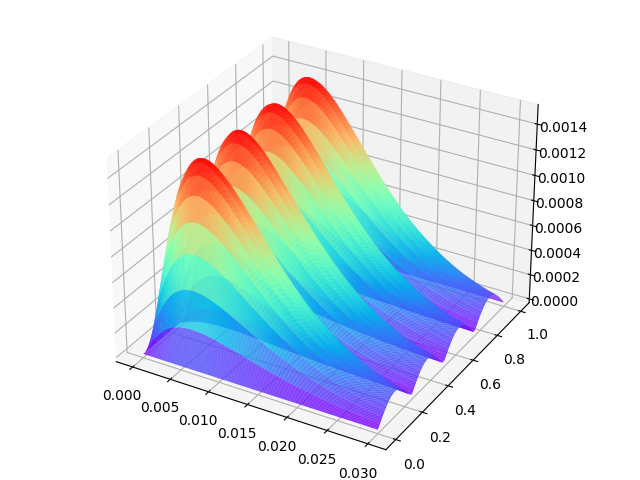
当取不同的$\tau,h$时，计算得到的误差如下表所示。
| $\tau$ | $h$ | 误差$e$ | $e_i/e_{i+1}$ |
|---|---|---|---|
| $\frac{1}{10}$ | $\frac{1}{10}$ | 0.0428079643162558 | |
| $\frac{1}{40}$ | $\frac{1}{20}$ | 0.00951825176096948 | 4.4975 |
| $\frac{1}{160}$ | $\frac{1}{40}$ | 0.00244056613219328 | 3.9000 |
| $\frac{1}{640}$ | $\frac{1}{80}$ | 0.000606385251482932 | 4.0248 |
| $\frac{1}{2560}$ | $\frac{1}{160}$ | 0.000151362159712509 | 4.0062 |
我们知道最简显格式的误差为$||[u]^k-u^k||=O(\tau + h^2)$，设$e_i=C \times (\tau_i + h_i^2)$， 取$\tau_{i+1}=\frac{1}{4} \tau_i$,$h_{i+1}=\frac{1}{2}h_i$，可以得到$\frac{e_i}{e_{i+1}} =4$，与上表结果相符，从而也验证了最简显格式的误差阶数为$O(\tau + h^2)$.