排序算法

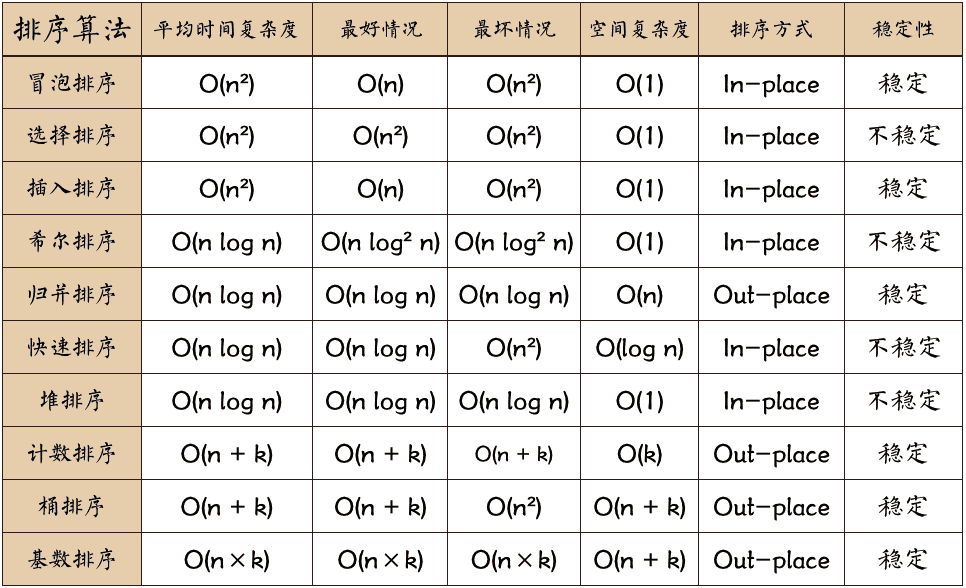
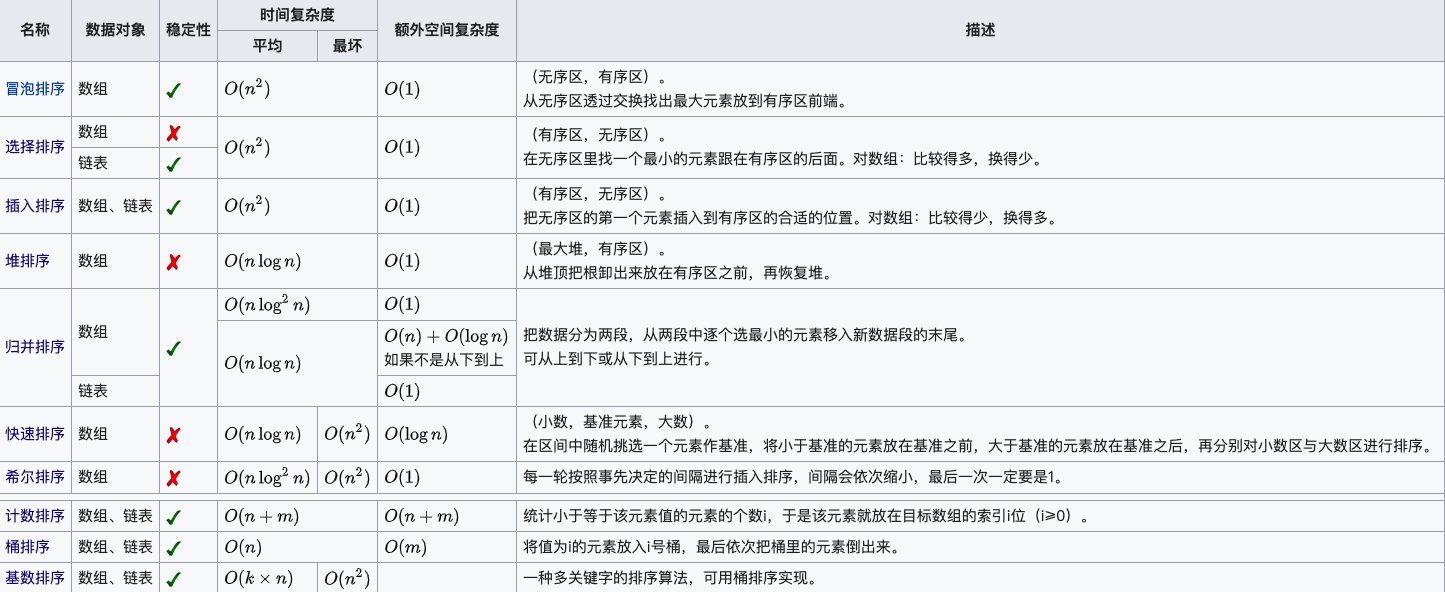
冒泡排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class BubbleSort {
    public int[] sort(int[] sourceArray) {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        for (int i = 1; i < arr.length; i++) {
            // 设定一个标记，若为 true，则表示此次循环没有进行交换，也就是待排序列已经有序，排序已经完成
            boolean flag = true;

            for (int j = 0; j < arr.length - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;

                    flag = false;
                }
            }

            if (flag) {
                break;
            }
        }
        return arr;
    }
}

选择排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
public class Selection {
    public static void sort(Comparable[] a) {
        // 将 a[] 按升序排列
        int N = a.length;
        for (int i = 0; i < N; i++) {
            // 将 a[i] 和 a[i + 1 ... N] 中最小的元素交换
            int min = i;    // 最小元素的索引
            for (int j = i + 1; j < N; j++) {
                if (less(a[j], a[min])) min = j;  // 找到a[i+1,...,N]中最小的元素
            }
            exch(a, i, min);
        }
    }
}

插入排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
public class Insertion {
    public static void sort(Comparable[] a) {
        // 将 a[] 按升序排列
        int N = a.length;
        for (int i = 1; i < N; i++) {
            // 将 a[i] 插入到 a[i - 1]、a[i - 2]、a[i - 3]...之中
            // less(a[j], a[j - 1])，是如果 a[j] 比 a[j - 1] 小
            for (int j = i;  j > 0 && less(a[j], a[j - 1]); j--) {
                exch(a, j, j - 1);
            }
        }
    }
}

希尔排序

希尔排序的思想是使数组中任意间隔 h 的元素都是有序的。希尔排序更高效的原因是它权衡了子数组的规模和有序性。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
public class Shell {
    public static void sort(Comparable[] a) {
        // 将 a[] 按升序排列
        int N = a.length;
        int h = 1;
        while (h < N/3) h = 3 * h + 1; // 1, 4, 13, 40, 121, 364, 1093, ...
        while (h >= 1) {
            // 将数组变为 h 有序
            for (int i = h; i < N; i++) {
                // 将 a[i] 插入到 a[i - h], a[i - 2 * h], a[i - 3 * h]...之中
                for (int j = i; j >= h && less(a[j], a[j - h]) ; j -= h) {
                    exch(a, j, j - h);
                }
                h = h / 3;
            }
        }
    }
}

归并排序

归并排序将数组分成两个子数组分别进行排序，并将有序的子数组归并以将整个数组排序，递归调用发生在处理整个数组之前。

原地归并的抽象方法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
public static void merge(Comparable[] a, int lo, int mid, int hi) {
    // 将a[lo,...,mid]和a[mid + 1,...,hi]归并
    int i = lo, j = mid + 1;
    for (int k = lo; k <= hi; k++) { // 将a[lo,...,hi]复制到aux[lo,...,hi]
        aux[k] = a[k];
    }
    for (int k = lo; k <= hi; k++) { // 归并回到a[lo,...,hi]
        if (i > mid)                    a[k] = aux[j++];
        else if (j > hi)                a[k] = aux[i++];
        else if (less(aux[j], aux[i]))  a[k] = aux[j++];
        else                            a[k] = aux[i++];
    }
}

自顶向下的归并排序：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
public class Merge {
    private static Comparable[] aux; // 归并所需的辅助数组
    public static void sort(Comparable[] a) {
        aux = new Comparable[a.length]; // 一次性分配空间
        sort(a, 0, a.length - 1);
    }
    private static void sort(Comparable[] a, int lo, int hi) { // 将数组a[lo,...,hi]排序
        if (hi <= lo) return;
        int mid = lo + (hi - lo) / 2;
        sort(a, lo, mid);       // 将左半边排序
        sort(a, mid + 1, hi);   // 将右半边排序
        merge(a, lo, mid, hi);  // 归并结果
    }
}

快速排序

快速排序将数组排序的方式是当两个子数组都有序时整个数组也就自然有序了，递归调用发生在处理整个数组之后。

首先是切分算法，使得 a[lo...j-1] <= a[j] <= a[j+1...hi]，返回指标j。实现切分算法的思路是先随机地取a[lo]作为切分元素，然后我们从数组的左端开始向右扫描直到找到一个大于等于它的元素，再从数组的右端开始向左扫描直到找到一个小于等于它的元素，交换它们的位置。如此继续，我们保证左指针i的左侧元素都不大于切分元素，右指针j的右侧元素都不小于切分元素。当两个指针相遇时，将切分元素a[lo]和左子数组最右侧的元素a[j]交换后返回j即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
private static int partition(Comparable[] a, int lo, int hi) {
    // 将数组切分为 a[lo,...,i - 1], a[i], a[i + 1,...,hi]
    int i = lo, j = hi + 1; // 左右扫描指针
    Comparable v = a[lo];   // 切分元素
    while (true) {
        // 扫描左右，检查扫描是否结束并交换元素
        while (less(a[++i], v)) if (i == hi) break;
        while (less(v, a[--j])) if (j == lo) break;
        if (i >= j) break;
        exch(a, i, j);
    }
    exch(a, lo, j); // 将 v = a[j] 放入正确的位置
    return j;
}

快速排序算法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
public class Quick {
    public static void sort(Comparable[] a) {
        StdRandom.shuffle(a); // 消除对输入的依赖
        sort(a, 0, a.length - 1);
    }
    private static void sort(Comparable[] a, int lo, int hi) {
        if (hi <= lo) return;
        int j = partition(a, lo, hi);  // 即切分算法
        sort(a, lo, j - 1); // 将左半部分 a[lo,...,j - 1]排序
        sort(a, j + 1, hi); // 将右半部分 a[j + 1,...,hi]排序
    }
}

快速排序中重要的就是切分算法，切分算法还有三向切分。维护一个指针lt使得a[lo,...,lt-1]中的元素都小于v，一个指针gt使得a[gt+1,..,hi]中的元素都大于v，一个指针i使得a[lt,...,i-1]中的元素都等于v。

三向切分的快速排序:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
public class Quick3way {
    private static void sort(Comparable[] a, int lo, int hi) {
        if (hi <= lo) return;
        int lt = lo, i = lo + 1, gt = hi;
        Comparable v = a[lo];
        while (i <= gt) {
            int cmp = a[i].compareTo(v);
            if      (cmp < 0) exch(a, lt++, i++);
            else if (cmp > 0) exch(a, i, gt--);
            else              i++;
        } // 现在 a[lo,...,lt-1] < v = a[lt,...,gt] < a[gt+1,...,hi] 成立
        sort(a, lo, lt - 1);
        sort(a, gt + 1, hi);
    }
}

三向切分相关LeetCode题目：

75.颜色分类

LeetCode排序练习

912.排序数组