本篇是博客《The Incredible Machine》的笔记,文章通过一个数独的故事来解释什么是零知识证明。
先总结一下这个过程:
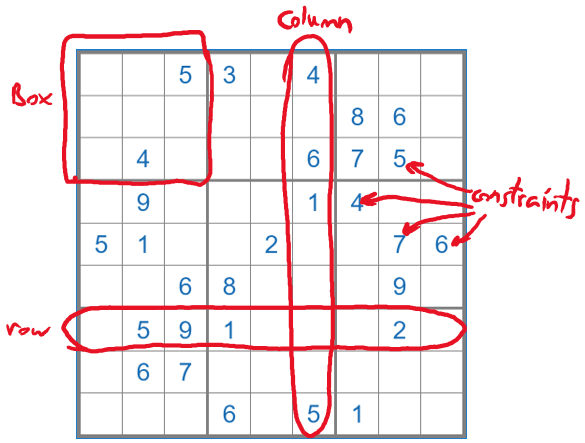
- 交互式证明。Alice知道数独的解,先将答案写在纸上,然后盖住,Bob发起一个随机挑战,可以选择行、列或者一个3 $\times$ 3的块。如果选择行,那么收集每行的纸片到一个袋子里,混合后,每个袋子打开都是1~9的数字。重复此过程让我们理由相信Alice知道数独的解,并且这一过程没有泄漏解。
- 模拟。上述过程在Alice和Bob事先商定随机挑战选择的顺序后,可以在不知道数独解的情况下通过挑战。这也正好证明了这一过程是零知识的。
- 非交互式证明。由一个机器来模拟这一过程,机器内部事先焊一个随机挑战的顺序,这个顺序可以由一个仪式来完成,保证没有人知道这个顺序。这个机器也是存在缺点的,可以通过实验得到这个随机顺序。
正文如下:
How Alice, Bob, and Charlie used Zero-Knowledge and Blockchains to launch The Global Sudoku Revolution.
This post is inspired by two great papers that make zero-knowledge proofs accessible to a wide audience:
[1] How to Explain Zero Knowledge Protocols to Your Children (Quisquater et. al.)
[2] Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles (Gradwohl et. al.).
Alice, Bob, and Charlie loved to solve Sudoku problems.The three friends liked challenging each other with puzzles all the time (in fact, sometimes they solved Sudoku problems that were REALLY large — not just 9x9 taken from here). Alice was the cleverest of the three. She would draw a Sudoku board on paper, and fill in some of the constraints. Then, she’d let Bob and Charlie try to solve the puzzle.
The Proof
One day, Bob, who was working on an especially difficult Sudoku that Alice had devised(设计的) sighed with despair(绝望的). “I swear, this puzzle has no solution! Alice just gave me one of the unsolvable ones to mess with me!”
He quickly came to Alice to complain.
“I’ll prove to you that this puzzle has a solution, and that I know it!” declared Alice. “Good!” Said Bob, who was secretly hoping to learn the answer and later taunt(嘲讽) Charlie with it.
“In fact, I’ll prove it to you with ‘zero-knowledge’, that is, without ever revealing the solution itself”. “I’d like to see you try”, said Bob, who was still thinking of all the fun he’d have teasing (戏弄)Charlie.
The Commitment
Alice retrieved 81 blank index cards. She quickly wrote a single digit (from 1 to 9) on each card and carefully placed the cards on the table, in a 9-by-9 matrix, organized just like a Sudoku puzzle. All of the cards were placed face down, with the exception of the few that had the constraints that Bob had already seen written on them.

随机选择行、列或者一个块来进行验证。
The Random Challenge
Bob was excited. The solution was close. He’d been working on the problem for ages!
“Bob, you aren’t allowed to peak at the cards!” Alice exclaimed to Bob’s disappointment. “Not yet anyway. But I will let you test the solution. You can choose whether you want to check the rows, the columns, or the blocks. Pick one at random.”
Bob decided to pick the rows. Alice proceeded to place the cards from each row inside an opaque bag — one bag per row. She gave each bag a thorough shake, making sure the index cards inside were mixed well. She handed the bags to Bob, who gave her a quizzical look.
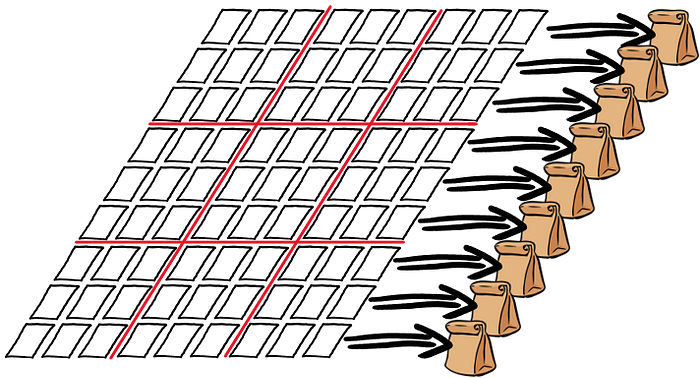
Verification
“Well, open them!” she said. “They should each have exactly 9 cards with all the numbers 1 through 9”. Bob opened each bag and verified that this was indeed the case.

“This doesn’t prove a thing!” I can also do that! I’d just have to place the numbers 1 through 9 in each row in any order i’d like!” said Bob quickly.
Alice explained that she couldn’t have known in advance that Bob would pick the rows. She’s not a mind reader! In fact, only a correct solution would have the numbers 1–9 in each row, column, and box and so if her solution was not correct, Bob would have at least a 1 in 3 chance of catching her.
Rinse and Repeat
Bob thought that a 1 in 3 chance of catching Alice wasn’t good enough. He still had a gnawing suspicion that the puzzle was unsolvable. He demanded that Alice repeat the procedure with him — each time placing the same cards for the same Sudoku problem face down on the floor, but letting him pick a different test at random. After a long series of tests, Bob was forced to admit that Alice was either an extremely lucky person, or, that she simply has a solution to the Sudoku problem (or perhaps she could read his thoughts after all). He was also quite disappointed that he had gained no knowledge (zero-knowledge) about the solution. All he knew after all these tests was that it was highly likely that every row, column and block did indeed contain the numbers 1–9 exactly once, which could only be so if Alice knew the solution.
The three friends had made it a habit to prove to one another that their Sudoku challenges were solvable. After all, no one wants to spend his time on an unsolvable problem. Each test was long and quite exhausting, but Sudoku is after all very serious business.
如果只进行一次验证,那么Alice可能会有1/3概率作弊,因此需要重复进行随机试验,提高可信度。
Blockchains and The Global Sudoku Revolution
One day, Alice had a great idea. Knowing that her love for Sudoku is shared by millions online, she decided to open her very own YouTube channel, where she can post her own Sudoku challenges online. She called it “The Sudoku Blockchain” (she didn’t know what blockchains were exactly, but it was such a cool buzzword(时髦术语,流行行话)). She dreamed of many channel subscribers that would send her Bitcoins and decided to include features that the competing Sudoku channels did not have: She asked Bob to verify the existence of a solution to each of the puzzles using a zero-knowledge proof. She’d film the whole thing and put it on the Sudoku Blockchain, so that everyone would know that (with high probability) each of the puzzles is indeed solvable.
The Simulation
One day, Alice came over to Bob’s house to record the proof for a Sudoku challenge, but found that she left the solution to the puzzle at home. Since she was in a hurry to publish the new challenge online, she begged Bob to film it with her anyway. She convinced Bob to pretend to run the proof with her. Together they agreed on a sequence of tests (rows / columns / and blocks) that Bob would “randomly” pick. Since Alice too knew the sequence of tests, she could easily pass them without having the solution to the puzzle.
Charlie, who was travelling abroad and saw the video was later surprised when Alice and Bob told him how they filmed it. “I’ll never trust you two again!” he exclaimed. “No one should trust any of your online video proofs!”.
模拟,在模拟情况下有一种超能力,事先约定“随机”选择的顺序,不知道真正的解也能通过测试,这不正恰好说明没有泄漏知识嘛!
The Incredible Machine and Non-Interactive Proofs
Charlie was frustrated. He did not want to easily give up his Sudoku solving habit, but knowing that Alice and Bob were not trustworthy, he wanted a way to check proofs remotely. After a few sleepless nights, he declared to Alice and Bob that he had a new idea. He locked himself in his room for hours and labored frantically through the night. In the morning, Charlie presented Alice and Bob with his incredible new invention: “The Zero-Knowledge Sudoku Non-Interactive Proof Machine” (or zk-SNIPM as he like to refer to it).
The Machine was basically an automated version of Alice’s test. Alice would need to place her cards on the conveyor belt, and feed Sudoku solutions to the machine. The machine would then collect the cards from rows, columns, or boxes and place them automatically into bags that would come out on the other side (after being thoroughly mixed). Then, Alice could open the bags while the camera was still rolling and reveal their contents.
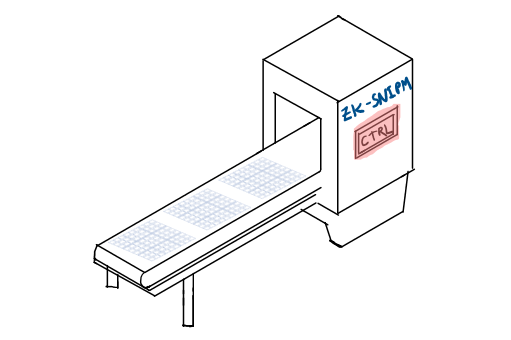
The machine had a control panel with a long series of dials that set the test for each set of 81 cards that Alice would feed in. Charlie had set up his own secret series of tests and then welded the control panel’s cover shut (Alice was worried that he also booby-trapped it with explosives, or filled it up with scorpions, vials of acid, or some other similarly nasty thing. Charlie was a bit extreme when it came to securing his devices).
Charlie could now trust his machine to provide a series of tests that was unknown to Alice so that he could watch youtube videos of proofs and be relatively sure that Alice had not cheated together with Bob.
The Ceremony
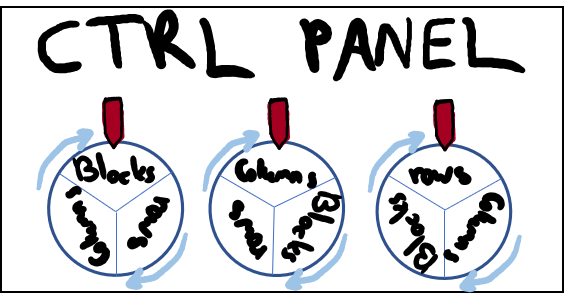
Alice and Bob were jealous of Charlie’s zk-SNIPM machine and wanted to use it to verify all puzzles (including those that Charlie invented). The only problem was that Charlie was the one who had set up the secret series of tests, and they could not let him use it for proofs (he could easily cheat since he knows the sequence of tests). Instead, Alice suggested that they conduct a multi-party set up of the machine together. A sort of “trusted setup ceremony”. She asked Charlie to open the control panel (and remove all of his nasty traps). Each of the dials on the control panel had 3 states, and you would need to rotate it to select the test.
She suggested that they place the machine in a dark room, and remove all the labels from the knobs. Each one of them would then go into the room with the machine in the dark (Bob also suggested that they’d be blindfolded just for good measure, and that they each wear a tinfoil hat to prevent mind reading side-channel attacks by Alice) and would turn the knobs on the machine to a random position (either turn them one-third of a turn clockwise, two-thirds of a turn clockwise, or leave them as they are). This way, the final setting of each knob would not be known to any single one of them (in fact, even if two participants colluded, they would not know the final state of the knob without the third person’s assistance). After the set-up ceremony was over, they’d weld the cover of the machine shut.
Cracking the Machine
One afternoon, when Bob and Charlie were off travelling, Alice was left alone with the machine. She started wondering if it was as secure as advertised. Thinking about it for a while she decided to feed it slightly modified Sudoku puzzle solutions in order to discover which tests the machine was using. She used a Sudoku puzzle that she could solve, and fed in many boards to see that the solution is indeed accepted by the machine. She then repeated the procedure, but changed the first board fed to the machine to simply include the numbers 1–9 in each row (without forming a legal solution in columns or boxes). The test still passed, and she then realized she can use this idea to learn the sequence of tests that were pre-set within the machine.
这里Alice先用一个数独的真解喂给机器,看看机器的输出结果。接着重复这一过程,但是修改解,保证每行是数字1~9,喂给机器,查看机器的输出结果,这样可以推测出之前通过仪式得到的随机顺序。
Alice felt very frustrated. Can you help Alice build a better zk-SNIPM? Can you think of a series of tests that would be harder to crack, or is the approach doomed to fail? Write us and tell us your ideas!
A Note About the Real World
In fact, the zk-SNIPM is a tongue-in-cheek construction of a non-interactive zero-knowledge prover, somewhere between zk-SNARKs and tamper-proof hardware. zk-SNIPM relies on a “physical” type of zero-knowledge proof. Such physical proofs could in fact be made much more powerful, for example, by using a photocopy machine to copy the cards and check the rows, columns and boxes simultaneously on the same solution. Still, we have elected to utilize a physical proving system that has some analogies to computational proofs found in cryptographic zero-knowledge constructions.
Alice’s initial proving method is analogous to an interactive zero-knowledge proof protocol, where the verifier sends a random challenge to the prover, after she commits to the solution. A prover and verifier that are colluding and share this random challenge in advance can simulate a proof, without really knowing the solutions. A non-interactive version that must work without this challenge step, is constructed by hiding the challenge itself in some cryptographic “machinery” in advance. This prevents the prover from having access to the challenge. Indeed, one good way to generate such a trusted challenge is through a “ceremony” enacted through multiparty computation that combines the randomness from several participants into a single random challenge, encoded in the proving system.
开始的证明方法类似交互式零知识证明协议,验证者给证明方一个随机挑战,然后进行验证。证明方和验证方可以事先作弊商量随机挑战的顺序,这样他们在不知道解的情况下可以模拟一个证明。后来的机器验证过程是非交互式证明,实现构造一个随机顺序,可以通过仪式的方式,然后再进行证明。
The Sudoku example in this post is taken in slightly modified form from Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles (Gradwohl et. al.).
Many thanks to Daniel Benarroch for his help with this post.
This post was originally published on qed-it.com.
