本篇博客记录了安比实验室知识证明介绍系列文章的笔记。几篇文章如下:
初识「零知识」与「证明」
原文链接:初识「零知识」与「证明」。
文章先介绍了“证明”的历史。
- 古希腊:「证明」 == 「洞见」
- 二十世纪初:「证明」 == 「符号推理」
- 六十年代:「证明」 == 「程序」
- 八十年代:「证明」 == 「交互」,拓宽了「证明」的概念。通过构造两个图灵机进行「交互」而不是「推理」,来证明一个命题在概率上是否成立。
零知识证明有什么用处?
零知识证明技术可以解决数据的信任问题,计算的信任问题!
零知识证明技术可以「模拟」出一个第三方,来保证某一个论断是可信的。
换句话说,当我们收到一个加了密的数据, 然后还有一个零知识证明。这个零知识证明是说 「关于数据的 X 断言成立」,那么这等价于有一个天使在我们耳边悄声说,「关于数据的X 断言成立」!
对于这个 X 断言,可以非常灵活,它可以是一个 NP复杂度的算法。大白话讲只要我们能写一段程序(一个多项式时间的算法)来判断一个数据是否满足 X 断言,那么这个断言就可以用零知识证明的方式来表达。通俗点讲,只要数据判定是客观的,那么零知识证明就适用。
零知识证明的用处:
- 数据的隐私保护
- 计算压缩与区块链扩容
- 端到端的通讯加密
- 身份认证
- 去中心化存储
- 信用记录
- 构造完全公平的现实数字化商品的交易协议
知识和信息的区别:
- 「知识」是与「计算难度」相关,而「信息」则不是
- 「知识」是与公共所知的东西有关,而「信息」主要与部分公开的东西有关
可验证计算与电路可满足性问题:
另外电路可满足问题和地图三染色问题一样,是NP-Complete问题。NP-Complete 是一类问题,他的求解过程是多项式时间内难以完成的,即「求解困难」,但是验证解的过程是多项式时间可以完成的,即「验证简单」。
所谓的电路可满足性就是指,存在满足电路的一个解。如果这个解的输出值等于一个确定值,那么这个解就能「表示」电路的计算过程。
「零知识的电路可满足性证明协议」提供了一种最直接的保护隐私/敏感数据的技术
从「模拟」理解零知识证明:平行宇宙与时光倒流
原文链接:从「模拟」理解零知识证明:平行宇宙与时光倒流。
安全的定义与不可区分性
这一部分是密码学中的知识。
一切安全都有前提的。只有经过数学证明之后,大家才能够确信这个 算法/方案 的安全性基于一些非常明确的「安全假设」。
完美安全:假设你是一个攻击者,你通过密文获取不到任何有价值的信息,破解的唯一手段就是靠瞎蒙。
📝 在Dan Boneh and Victor Shoup 的 《A Graduate Course in Applied Cryptography》书中定义为:
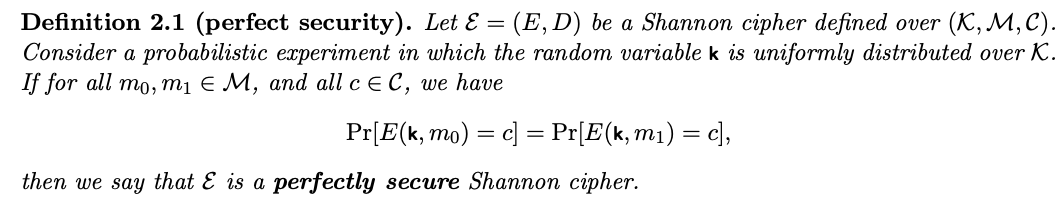
通过密文获取不到信息,这就意味着你没有获得任何额外的计算能力,能够帮助让你以更短的时间来计算出明文。
语义安全:假设你是一个攻击者,你通过密文在多项式时间内计算不出来任何有价值的信息。
📒书中定义为:

不可区分的概念: 我们又引入一个概念——「不可区分性」,来重新表述加密算法的安全性:假设你是一个攻击者,而我有一个加密算法:
- 你随机产生两段等长的明文,
m1=「白日依山尽,黄河入海流」,m2=「烫烫烫烫烫,烫烫烫烫烫」 - 你把这两段明文,
m1与m2交给我 - 我随机挑选一个明文,不告诉你是哪一个,然后进行加密,产生一个密文
c - 我把密文
c出示给你看,让你猜这个c究竟是由唐诗加密产生,还是乱码加密产生 - 如果你用一台计算机来破解
c,在多项式时间内破解不出来,也就是说你没办法区分c的来源,那么就说明加密算法是语义安全的
区分两个世界
证明的零知识过程,等价于构造(寻找)一个「模拟」算法,这个算法能够让模拟器来模拟出一个「没有知识」的理想世界。如果这个算法存在,而且两个世界不可区分,那么就证明完毕。
所谓的不可区分性针对的是理想世界中的个体认知而言。而「可区分性」是对位于世界外部的神而言。
首先「零知识」是为了保护 Alice 的利益,因为 Alice 不想在交互过程中透露更多的信息给 Bob,不想让 Bob 知道她所拥有的秘密 w,甚至不想让 Bob 从交互的过程中分析出哪怕一丁点的信息。那么怎么保证这一点呢?「模拟器」这时候登场了,它能模拟出一个和现实世界外表一模一样的「理想世界」,然后「模拟器」在这个世界中可以轻松地骗过任何一个对手,让对方无法分辨自己是在现实世界中,还是理想世界中。因为「模拟器」手里没有那个秘密 w,「理想世界」是零知识的。又因为两个世界的不可区分性,所以我们可以得出结论:Alice 的交互协议是「零知识」的。
地图三染色问题的零知识证明
文章中用图片形象的说明了零知识证明的过程。不过这是针对诚实的Bob,如果是不诚实的Bob呢?如果在模拟器第一次实施时间倒流之后,Bob又选择了不同的边,那么模拟器可以把颜色打乱之后,再次运行时间倒流,在多次时间倒流之后,Bob 极大的概率总会一次选择模拟器进行染色的那条边,然后这时候模拟器才走到第三步,打开纸片。
阿里巴巴、洞穴与芝麻开门
文章中再次阐述了阿里巴巴与大盗的故事,这个故事来源于论文How to explain zero-knowledge protocols to your children,我的论文的笔记见这里。The Jealous Reporter用的剪辑手段就是模拟器中的超能力,由于两家电视台放出的影片人们无法区分,而假的那个根本不知道洞穴的秘密,这也就证明了这个过程是零知识的。
模拟器与图灵机
模拟器不能随便开挂。模拟器其实只是一个图灵机,而前面提到的时间倒流是图灵机可以实现的功能。
文章中下面这段话很重要👇
证明零知识的过程,就是要寻找一个算法,或者更通俗点说,写出一段代码,它运行在外部计算机系统中,但是实现了虚拟机的功能。而且在虚拟机中,需要有一个不带有「知识」作为输入的 Zlice,可以骗过放入虚拟机运行的 Bob。
读心术:从零知识证明中提取「知识」
这篇文章实际是在说明零知识证明中的可靠性。
「零知识」vs. 「可靠性」 「零知识证明」并不是通过给出一个不允许发生的事件列表来定义,而是直接给出了一个最极致的「模拟条件」。
所谓「模拟条件」是指,通过「模拟」方法来实现一个「理想世界」,使之与「现实世界」不可区分;而由于在理想世界中不存在知识,所以可以推导出结论:现实世界满足「零知识」。
我们继续分析下一个交互系统(安全协议)的三个性质:「完备性」、「可靠性」与「零知识」。
可靠性(Soundness):Alice 在没有知识的情况下不能通过 Bob 的验证。
完备性(Completeness):Alice 在有知识的情况下可以通过 Bob 的验证。
零知识(Zero-knowledge):Alice 在交互的过程中不会泄露关于知识的任何信息。
我们可以看出来「可靠性」和「完备性」有一种「对称性」。可靠性保证了恶意的 Alice 一定失败,而完备性保证了诚实的 Alice 一定成功。
简洁的Schnorr协议
📝 这一小节的内容补充了关于群的知识。
Alice 拥有一个秘密数字,a,我们可以把这个数字想象成「私钥」,然后把它「映射」到椭圆曲线群上的一个点 a*G,简写为 aG。这个点我们把它当做「公钥」。
sk = aPK = aG
请注意「映射」这个词,我们这里先简要介绍「同态」这个概念。椭圆曲线群有限域之间存在着一种同态映射关系。有限域,我们用 Zq这个符号表示,其中素数 q是指有限域的大小,它是指从 0, 1, 2, …, q-1 这样一个整数集合。而在一条椭圆曲线上,我们通过一个基点,G,可以产生一个「循环群」,标记为 0G, G, 2G, …, (q-1)G,正好是数量为 q个 曲线点的集合。任意两个曲线点正好可以进行一种「特殊的二元运算」,G + G = 2G,2G + 3G = 5G,看起来这个二元运算好像和「加法」类似,满足交换律和结合律。于是我们就用 +这个符号来表示。之所以把这个群称为循环群,因为把群的最后一个元素 (q-1)G,再加上一个 G就回卷到群的第一个元素 0G。
给任意一个有限域上的整数 r,我们就可以在循环群中找到一个对应的点 rG,或者用一个标量乘法来表示 r*G。但是反过来计算是很「困难」的,这是一个「密码学难题」—— 被称为离散对数难题[2]。
也就是说,如果任意给一个椭圆曲线循环群上的点 R,那么到底是有限域中的哪一个整数对应 R,这个计算是很难的,如果有限域足够大,比如说 256bit 这么大,我们姑且可以认为这个反向计算是不可能做到的。
Schnorr 协议充分利用了有限域和循环群之间单向映射,实现了最简单的零知识证明安全协议:Alice 向 Bob 证明她拥有 PK 对应的私钥 sk。
z 的计算和验证过程很有趣,有几个关键技巧:
- 首先 Bob 必须给出一个「随机」挑战数,然后 Bob 在椭圆曲线上同态地检查
z。如果我们把挑战数c看成是一个未知数,那么r+a*c=z可以看成是一个一元一次方程,其中r与a是方程系数。请注意在c未知的前提下,如果r + a*x = r' + a'*x要成立,那么根据 Schwatz-Zippel 定理[3],极大概率上r=r',a=a'都成立。也就是说, Alice 在c未知的前提下,想找到另一对不同的r',a'来计算z骗过 Bob 是几乎不可能的。这个随机挑战数c实现了r和a的限制。虽然 Bob 随机选了一个数,但是由于 Alice 事先不知道,所以 Alice 不得不使用私钥a来计算z。这里的关键:c必须是个随机数。 - Bob 验证是在椭圆曲线群上完成。Bob 不知道
r,但是他知道r映射到曲线上的点R;Bob 也不知道a,但是他知道a映射到曲线群上的点PK,即a*G。通过同态映射与Schwatz-Zippel 定理,Bob 可以校验z的计算过程是否正确,从而知道 Alice 确实是通过r和a计算得出的z,但是又不暴露r与a的值。 - 还有,在协议第一步中产生的随机数
r保证了a的保密性。因为任何一个秘密当和一个符合「一致性分布」的随机数相加之后的和仍然符合「一致性分布」。
📝 c必须是随机数。
再遇模拟器
其实,「可靠性」和「零知识」这两个性质在另一个维度上也是存在着一种对称性。**可靠性保证了恶意的 Alice 一定失败,零知识保证了恶意的 Bob 一定不会成功。**有趣地是,这种对称性将体现在模拟出来的「理想世界」中。
