论文见Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles。本篇论文详细的介绍了关于数独问题的密码学和物理上的零知识证明协议。可以了解到零知识证明协议的完整过程，一般步骤有哪些。

1 Introduction

如何在不透露解的情况下让别人相信你知道一个数独的解。关注两件事，证明者如何说明：

1. 给定一个数独问题，存在一个解
2. 他知道这个解，但是不用给出关于解的任何其他信息

数独问题在计算复杂度上属于NP问题，事实上，是NP-完全问题。NP问题意味着很容易验证一个解是否正确。

2 Definitions

一般化的数独问题，数独问题的大小是 $n = k^2$，总共 $n \times n$个格子，每个小块是 $k \times k$大小的，那么数的范围是 ${ 1, …, n}$。比如常见的 $k = 3$，$9 \times 9$ 大小的数独。一个具体数独问题例子和解都是 $O(n^2 \log n)$ 位的。

Cryptographic Functionalities

协议中有两方，一个是prover，一个是verifier。一旦prover和verifier固定下来，他们交互发的消息可以看作是一个只包含prover和verifier随机数的函数。下面讨论这个协议的一些性质：

1. completeness.

   一个诚实的verifier会accepect一个正确的证明。也就是一个prover有一个合法的解会遵循这个协议。

2. soundness error.

   The soundness error (or soundness) of the protocol is the (upper bound on the) probability that a verifier accepts an incorrect proof, i.e. a proof to a fallacious statement; in our case this corresponds to the event that a prover who does not a solution to a given Sudoku puzzle, claims that it knows to solve it, and the verifier accepts this claim.

   对于错误的证明，会有多少的概率通过verifier的验证。

3. zero-knowledge.

   The goal in designing the protocols is to prevent the verifier from gaining any new knowledge from a correct (interactive) proof. I.e., the protocol should be zero- knowledge in the following sense: whatever a verifier could learn by interacting with the correct prover, the verifier could learn itself.

   什么是零知识呢？无论verifier通过与prover交互学到了什么，那么verifier也能通过和自己交互学到这些知识，才是真的没有泄露任何别的知识。实际操作中有一个有效的模拟器。这个模拟器会生成verifier和prover之间的对话，同时只知道puzzle，而不知道数独的解。要求模拟器中verifier与prover对话之间的分布和真实的情况下两者之间的分布是一样的，这样就无法区分模拟器和真实的情况。

4. proofs-of-knowledge.

   Our protocols should also be proofs-of-knowledge: if the prover (or anyone imper- sonating him) can succeed in making the verifier accept, then there is another ma- chine, called the extractor, that can communicate with the prover and actually come up with the solution itself. This must involve running the prover several times using the same randomness (which is not possible under normal circumstances), so as not to contradict the zero-knowledge properties.

   证明prover确实有知识，存在这样一个提取器，它能够通过和prover交互得到知识，当然，它不能发送通常的随机数，它可以多次使用相同的随机数。

论文中证明中用到的唯一的密码学工具是 commitment protocol。一个承诺协议，发送方向接收方承诺一个值，接收方不会学到任何关于这个值有用的信息。这样的一个协议包含两个阶段：

1. commit phase 承诺阶段。

   发送方绑定一些值 $v$，接收方不能决定任何关于 $v$ 有用的信息。特别地，对于任意的$b$和$b’$，接受方无法区分$v=b$和$v=b’$。这个性质称为 hiding。

2. decommit or reval phase

   接收方获得$v$后，确保它是原来的值，也就是说，一旦commit阶段结束，接收方会在reval阶段接收一个唯一的值。这个性质称为 binding。

bit commitment可以高效执行。

Physical Protocols

在文章中使用 tamper-evident sealed envelopes，也就是防拆封信封。在数独的例子中，每个盖住的卡片当作是这样的 tamper-evident sealed envelopes，将卡片翻开就相当于拆开信封。

3. Cryptographic Protocols

verifer要保证两件事情：

1. 存在一个解
2. the prover 知道这个解

零知识协议证明的结构：

1. The prover commits to several values. These values are functions of the instance, the solution and some randomization known only to the prover. 证明方承诺一些值。
2. The verifier requests that the prover open some of the committed values—this is called the challenge. The verifier chooses the challenge at random from a collec- tion of possible challenges. 验证方发起挑战。
3. The prover opens the requested values. 证明方打开要求的值。
4. The verifier checks the consistency of the opened values with the given instance, and accepts or rejects accordingly. 验证方验证给定实例打开值的一致性，然后相应地接受或者拒绝。

要求在步骤3中打开的值的分布是一个关于数独问题和步骤2中发送的挑战的有效函数。那么结合承诺协议的不可区分性质，说明了有效模拟器的存在性。

模拟器的操作如下：在步骤2中随机选择一个验证方可能发起的挑战，计算步骤1中会满足挑战的值。模拟器模拟将这些值发送给验证方，然后运行验证方的算法，用刚刚得到的值和数独问题作为输入。模拟器会获得在步骤2中发送的挑战。如果这个挑战是它之前猜的值，模拟器就会打开之前发送的承诺，那么验证方自然会接受，模拟器可以继续执行这个协议，否则的话，模拟器会重置并重新开始。这里有点绕，原文如下：

The simulator operates in the following way: it picks at random a challenge that the verifier might send in Step 2 (i.e. it guesses what the verifier’s challenge will be), and computes commitments for Step 1 that will satisfy this challenge. The simulator simulates sending these commitments to the verifier, then it runs the verifier’s algo- rithm with the puzzle as its input, a fresh set of random bits and these commitments being the first message it receives. It then obtains the challenge the verifier sends in Step 2. If this challenge is indeed the value it guessed, then the simulator can open the commitments it sent and the verifier should accept; the simulator can continue simulating the protocol and output the transcript of the simulated protocol execution. Otherwise, the simulator resets the simulation and starts it all over again.

如果可能的挑战的数量是多项式的，那么每次模拟器猜测验证方的挑战，就是用“reasonably high”概率是正确的。这个过程保证了协议是零知识的，因为模拟器的输出和验证方从证明方交互得到的输出是不能区分的，但是模拟器这一过程的计算是没有和证明方交互的，那肯定不能得到任何关于解的知识。

3.1 A Protocol Based on Coloring

对于3-Colorability Protocol，证明者重新排列颜色，然后提交每个顶点重新排列之后的颜色。验证方随机选择一条边，检查边的两端颜色是否是不同的。

对于数独问题，这个协议是如下这样的：

Prover步骤1是随机选择一个排列$\sigma$，从${1,\dots,n}$映射到${1,\dots,n}$，这样避免泄漏原来的解。

3.2 An Efficient Cryptographic Protocol with Constant Soundness Error

下面这种协议有常数的soundness error。这个协议的想法是将每个单元复制三份，创建关于解的行、列以及子网格的视角。复制后的每个单元随机排列，prover的工作是说明以下性质：

1. 对应行、列、子网格含有所有可能的数字，如${ 1,2,…,n }$。
2. 一个单元的三个版本的值都是相同的。
3. 这些复制后的单元中包含预先确定的值。

如果上述三个条件都满足的话，说明存在这样一个解并且prover是知道它的。具体的协议如下：

上面过程不是很好理解，例如$n=4$的情况，$3 \times n^2 = 2 \times 4^2 = 3 \times 16$，数独谜题里填的数字范围是 ${ 1,2,3,4 }$。这样有解的三个副本，分别是行、列、subgrids。

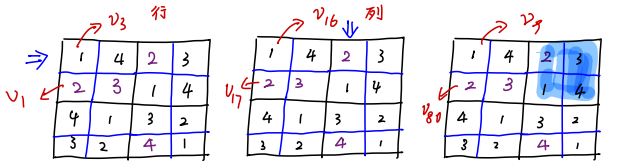
Prover：

1. 提交$3 \times n^2$ 个值 $v_1,v_2,…,v_{3 \times 4^2}$。$v_{i_1}、v_{i_2}、v_{i_3}$ 是原来数独解中的值，有相同的值，$(i_1,i_2,i_3)$ 是一个三元组，是随机的下标，例如图中的$(3,16,9)$、$(80,1,17)$。
2. 提交范围${ 1,2, \dots , 3 \times n^2 }$中 $n^2$个三元组$(i_1,i_2,i_3)$，例如${ (3,16,9),(80,1,17)\dots,(i_1,i_2,i_3), \dots }$。
3. 提交步骤2中个每个三元组的名字，如$(3,16,9)$的名字就是$(rows,columns,subgrids)$，$(80,1,17)$对应的是$(subgrids,rows,columns)$。
4. 提交步骤1中$3n$组位置，对应行、列和子网格，并且在每组中不会存在相交的两个单元格。例如图中蓝色箭头部分。

Verifier：选择以下三个中的一个进行挑战：

(a) 打开步骤1中$3 \times n^2$个值，以及步骤4中$3n$组的位置。验证每组中是否含有$n$个不同的值，任意两组之间不相交。

(b)打开步骤1中$3n^2$个值以及步骤2。验证提交的三元组对应下标的值都是相同的。

(c)打开步骤2、3、4中提交的值以及步骤1中已经填好的数独，如图中紫色数字。验证(i)打开的值和之前设定的值是一致的，(ii)步骤4中的每个集合和之前的位置是一致的，(iii)每个三元组的名字对应是正确的。

Overhead of our Protocols

上面两个协议都可以通过重复执行来降低soundness error。

4 Physical Protocols

物理上的协议，使用 Tamper Evidence作为物理的密码学基础，就是密封的信封。

密码学协议和物理的协议的还有一个不同是：

The protocol does not prevent cheating by adversaries that accept the risk of being labelled as cheaters (in this respect it is similar to the model of covert adversaries).

两个函数需要用到：shuffle 和 triplicate。

实现密封效果有三种方式：

1. 密封的信封
2. 刮刮卡
3. 验证方和证明方在同一个房间，用标准的不透明卡片，密封就是把数字盖着，揭开数字就是翻转卡片，将数字朝上。

协议3

Protocol 3 A physical protocol with 1/9 soundness error

• The prover places three scratch-off cards on each cell. On filled-in cells, he places three cards with the correct value, which are already open (scratched).
• For each row/column/subgrid, the verifier chooses (at random) one of the three cards of each cell in the corresponding row/column/subgrid.
• The prover makes packets of the verifier’s requested cards (i.e. for every row/ column/subgrid, he assembles the requested cards). He then shuffles each of the 3n packets separately (using the shuffle functionality), and hands the shuffled packets to the verifier.
• The verifier scratches off all the cards in each packet and verifies that each packet contains all of the numbers.

这个协议需要执行的洗牌次数比较多，对于$9 \times 9$的情况，需要进行$3 \times n = 3 \times 9 = 27$次洗牌，在实际操作中这个次数过多。

4.1.1 Reducing the Number of Shuffles

上面的意思是在验证阶段，prover给每个袋子标记一个值，从$0$到$c-1$，如果标记的是$0$表示这个口袋不被选中。那么对于每一个标记的号$i$，如果有$t$个袋子是这个标记，就把这$t$个袋子混合在一起进行洗牌操作，最后验证里面每个数字是否出现$t$次。这样就大大减少了shuffles函数的调用次数。

4.2 A Physical Zero-Knowledge Protocol with no Soundness Error

这种协议prover是没有办法作弊的。

4.3 A Protocol Using Scissors and a Sheet of Paper